Геометрические фракталы
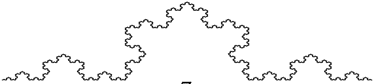
Снежинка Коха


Эта фигура — один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке.
Фрактальная размерность равна log4/log3 = log3(4) ≈ 1,261859... . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности.
Треугольник Серпинского
Фрактал, который был впервые описан в 1915 году польским математиком Вацлавом Серпинским.
При отображении он выглядит как треугольник, разделенный на четыре секции, каждая из которых составляет половину высоты и ширины оригинала.


Ковер Серпинского
Ковер (квадрат, салфетка) Серпинского. Квадратная версия была описана Вацлавом Серпинским в 1916 году. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата.
Разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов.
